MODÈLES (THÉORIE DES)

MODÈLES (THÉORIE DES)

«Modèle» est un terme qui appartient au vocabulaire de la plupart des sciences et qui a des significations multiples ^{[cf. MODÈLE]}. Ainsi, dans les sciences humaines, on entend généralement par modèle une théorie conçue pour expliquer un ensemble de phénomènes, alors qu’en logique mathématique on parle des modèles d’une théorie. Dans ce qui suit, il s’agira exclusivement des modèles et de la théorie des modèles de la logique mathématique. Toute étude des structures mathématiques dans laquelle les questions de langage interviennent de façon essentielle fait partie de la théorie des modèles, qui peut être considérée comme fille de la logique et de l’algèbre universelle.

Les racines de la théorie des modèles plongent dans l’enfance de la logique mathématique, puisque, dès 1915, Löwenheim donnait une formulation rudimentaire d’un des résultats fondamentaux du sujet, connu aujourd’hui comme le théorème de Löwenheim-Skolem.

Le mathématicien Thoralf Skolem découvre dès les années 1920-1934 plusieurs des idées fondamentales de la théorie, dont il est une manière de pionnier. Mais cette théorie ne sort vraiment des limbes que vers les années 1945-1950, grâce à A. Tarski (dont le séminaire à Berkeley «lance» la nouvelle discipline), A. Robinson, L. Henkin. À vrai dire, le mathématicien soviétique A. Mal’cev développait de son côté, avec une bonne dizaine d’années d’avance, nombre des mêmes idées que ses collègues occidentaux, mais ceux-ci ne prirent connaissance de ses travaux que beaucoup plus tard.

Une nouvelle étape est franchie au début des années 1960 (travaux de Vaught, Chang, Keisler, Morley, Kochen...) et, à partir de 1968 environ, la théorie des modèles connaît un véritable épanouissement.

Nous devrons nous contenter ici de présenter certains des principaux outils de la théorie, puis d’en exposer l’application à l’un de ses plus brillants résultats, le théorème de catégoricité de Morley. Enfin, nous mentionnerons quelques applications aux mathématiques, surtout à l’algèbre.

Le présent article prend la suite de l’étude sur le Calcul de prédicats du premier ordre du chapitre Les notions fondamentales: la logique du premier ordre de l’article LOGIQUE MATHÉMATIQUE, dont il conserve en particulier les notations. D’autre part, on trouvera à l’article ANALYSE NON STANDARD l’exposé d’une application fondamentale de la théorie et, à la fin de l’article RÉCURSIVITÉ, quelques indications sur son extension à des langages infinitaires.

Dès l’origine, la théorie des modèles s’est développée suivant deux axes principaux, selon le type de structures mathématiques auxquelles on songeait à l’appliquer. La problématique de ce que l’on peut appeler, pour être bref, l’école de Berkeley (Tarski et ses disciples, mais aussi, la géographie nonobstant, Skolem) provient de l’analyse, de la théorie des nombres et de la théorie des ensembles, tandis que l’école de Yale (A. Robinson et ses disciples, ainsi que Mal’cev) s’intéresse à l’algèbre. Pour les premiers, il n’y a pas lieu de borner la complexité des formules considérées, tandis que pour les seconds les formules à prendre en compte ont au plus deux blocs de quantificateurs de même nature (face=F0019 葉x ¹... 葉x ^p 說y ¹... 說y ^q , où est sans quantificateur: formules dites 葉說), voire un seul (face=F0019 說x ¹... 說x ^p : formules existentielles , ou 葉x ¹... 葉x ^p : formules universelles ). La plupart des résultats présentés dans les chapitres 1 et 2 appartiennent à la première tradition, tandis que le chapitre 3 se place davantage dans la seconde.

1. Quelques outils fondamentaux

Nous supposons connues ^{[cf. LOGIQUE MATHÉMATIQUE]} les notions de langage du premier ordre L, de L-structure (ou réalisation de L) et de satisfaction d’un énoncé 﨏 (formule close , c’est-à-dire sans variable libre) de L, dans une L-structure face=F9828 a, dite modèle de 﨏 (on note face=F9828 a = 﨏). Une théorie de L est, dans le présent contexte, exclusivement sémantique, définie comme un ensemble T d’énoncés de L qui admet un modèle (c’est-à-dire une L-structure satisfaisant tous les énoncés de T). La théorie d’une L-structure face=F9828 a est l’ensemble Th face=F9828 a des énoncés satisfaits dans face=F9828 a. Les théories de structure telles que Th face=F9828 a sont caractérisées par le fait qu’elles sont complètes , c’est-à-dire maximales pour l’inclusion, ou encore contenant, pour chaque énoncé 﨏, soit 﨏 soit la négation 囹 﨏. Enfin, deux structures face=F9828 a, face=F9828 b sont élémentairement équivalentes (on note face=F9828 a 令 face=F9828 b) si Th face=F9828 a = Th face=F9828 b, c’est-à-dire si, pour tout énoncé 﨏, face=F9828 a |= 﨏 équivaut à face=F9828 b |= 﨏. Il est clair que deux structures isomorphes (au sens mathématique usuel) sont élémentairement équivalentes, mais la réciproque est fausse: les ensembles Q et R munis de leur ordre habituel sont élémentairement équivalents et non isomorphes (pour une simple raison de cardinalité).

En théorie des modèles, les langages sont en général égalitaires (ils comportent un symbole de relation binaire distingué, l’égalité formelle ), ainsi que les structures (l’égalité formelle y est interprétée par l’identité). Aussi nous restreignons-nous dans cet article au cas égalitaire (clause désormais tacite). Nous notons |X| le cardinal d’un ensemble X.

Le théorème de compacité

La théorie des modèles a deux théorèmes fondateurs: le théorème de compacité (ou de finitude) et le théorème de Löwenheim-Skolem (descendant), tous deux très élémentaires. Le premier, qui intervient dans presque tous les résultats de théorie des modèles (sauf précisément dans le second), exprime le caractère fini de la propriété, pour un ensemble d’énoncés, d’admettre un modèle (égalitaire): «Un ensemble d’énoncés admet un modèle si et seulement si tous ses sous-ensembles finis admettent un modèle.»

Ce théorème, qui, par le détour de la syntaxe, n’est qu’une conséquence immédiate du théorème de complétude ^{[cf. LOGIQUE MATHÉMATIQUE]}, possède diverses démonstrations purement sémantiques, dont l’une, utilisant les ultraproduits, sera exposée au chapitre Ultraproduits .

Extensions, diagrammes, chaînes

Soit face=F9828 a et face=F9828 b deux L-structures d’univers A et B respectivement. Supposons que A 裂 B et, pour toute formule 﨏 de L à n variables libres sans quantificateur [resp. quelconque] et tout n -uple (a ¹, ..., a ⁿ ) d’éléments de A, que l’énoncé avec paramètres 﨏(a ¹, ..., a ⁿ ) soit satisfait dans face=F9828 a si et seulement si il l’est dans face=F9828 b. Alors face=F9828 a est appelé une sous-structure [resp. (sous-structure) élémentaire] de face=F9828 b, et face=F9828 b une extension [resp. élémentaire] de face=F9828 a. La notion de sous-structure subsume celle de sous-groupe, sous-espace vectoriel, sous-algèbre, etc. Mais en théorie des modèles (surtout de tradition tarskienne), la notion vraiment centrale est celle de sous-structure élémentaire.

L’une des méthodes pour construire une structure répondant à certaines exigences est de l’obtenir comme extension élémentaire convenable d’une structure donnée. D’où l’importance de la caractérisation suivante. Soit, dans un langage L(A) enrichi d’un symbole de constante c ^a pour chaque élément a de A, D(face=F9828 a) [resp. (face=F9828 a)] l’ensemble des énoncés sans quantificateur [resp. quelconques] satisfaits dans la L(A)-structure [ face=F9828 a, A] obtenue en enrichissant la L-structure face=F9828 a par l’interprétation de chaque c ^a par a . Une L-structure face=F9828 b est isomorphe à une extension [resp. élémentaire] de face=F9828 a si et seulement si il existe un enrichissement 麗 face=F9828 b, 縷 ^a 礪^a size=1^捻A de face=F9828 b qui est un modèle du diagramme [resp. élémentaire] D(face=F9828 a) [resp. (face=F9828 a)] de face=F9828 a.

Voici deux applications caractéristiques de cette méthode, dite méthode des diagrammes; elles reposent sur l’application du théorème de compacité à un ensemble d’énoncés de la forme X 聆 Y, où X est une théorie et Y le diagramme [élémentaire] d’une structure donnée:

Théorème (Mal’cev) . Soit K la classe des sous-structures de structures obtenues par appauvrissement à un langage L 裂 L de L -structures qui sont modèles d’une théorie T de L . Une L-structure face=F9828 a appartient à K si et seulement si toutes les sous-structures finiment engendrées de face=F9828 a appartiennent à K (autrement dit, K est de caractère fini).

Ce théorème a notamment permis à Mal’cev d’établir très simplement le caractère fini de diverses classes de groupes effectivement considérées en théorie des groupes.

Théorème de ^/Lo ご-Tarski . Soit T une théorie telle que toute sous-structure d’un modèle de T soit un modèle de T. Alors T équivaut à (i.e. a les mêmes modèles que) un ensemble d’énoncés universels. (La réciproque est évidemment vraie.)

Une méthode plus puissante consiste à construire une chaîne croissante 麗 face=F9828 a size=1^見 礪 size=1^見 size=1^麗 size=1^凞 d’extensions élémentaires et à considérer leur réunion: celle-ci est munie naturellement d’une L-structure qui en fait une extension élémentaire de chaque terme de la chaîne. À titre d’exemple, voici deux applications importantes de cette méthode:

Théorème de Chang-/Lo ご-Suszko . Soit T une théorie telle que la réunion d’une chaîne de modèles de T soit un modèle de T. Alors T équivaut à un ensemble d’énoncés 葉說. (La réciproque est immédiate.)

Théorème de cohérence de Robinson . Soit L¹ et L² deux langages, L leur intersection (c’est-à-dire l’ensemble des [formules écrites à l’aide des] symboles figurant dans L¹ et dans L²). Soit T une théorie complète de L, et ¹, ² des théories cohérentes de L¹, L², respectivement, contenant T. La théorie ¹ 聆 ² (de L¹ 聆 L²) est cohérente.

Les théorèmes de Löwenheim-Skolem

Dans sa première formulation, le théorème de Löwenheim-Skolem énonce qu’une théorie dans un langage dénombrable qui admet un modèle infini admet un modèle dénombrable.

Il découle immédiatement de ce résultat qu’une théorie qui admet un modèle infini a deux modèles non isomorphes. Il en est ainsi de la théorie de la structure standard de l’arithmétique, face=F9828 n = 麗N, +, 練, 0, 1 礪, ce qui a fait l’objet de discussions philosophiques qu’on ne peut rappeler ici. Il en est de même du «paradoxe de Skolem»: si la théorie axiomatique des ensembles ZF admet un modèle, elle admet un modèle dénombrable, lequel «contient» des ensembles non dénombrables tels que l’ensemble face=F9828 pN des ensembles entiers.

Il est facile de démontrer un théorème un peu plus général. Soit face=F9828 b un modèle infini d’une théorie T dans un langage dénombrable, 狀 un cardinal infini inférieur au cardinal |B| de l’univers de face=F9828 b. Il existe une sous-structure face=F9828 a de face=F9828 b qui est modèle de T et dont l’univers est de cardinal K. Montrons-le dans un cas particulier (mais caractéristique), où T est la théorie d’un corps commutatif face=F9828 b. Désignons par E un sous-ensemble de B de cardinal 見 et, pour tout sous-ensemble F de B, par F 漣 l’ensemble des éléments de B qui sont somme, produit, différence ou quotient de deux éléments de F.

Il est facile de vérifier que l’ensemble:

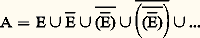est l’ensemble des éléments d’un sous-corps de face=F9828 b de cardinal 見.

Le lecteur aura sans doute remarqué que, dans le cas particulier de la théorie des corps commutatifs, le théorème de Löwenheim-Skolem ne lui apprend rien du tout: il est en effet immédiat que, pour tout ensemble X =x ⁱ, i 捻 I, de cardinal infini 見, le corps des fractions rationnelles Q(X) est de cardinal 見. Le corps:

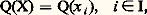a même une propriété supplémentaire assez particulière: les éléments x ⁱ y jouent tous le même rôle (ils sont indiscernables: cf. Classification des modèles et complexité d’une théorie ). On peut montrer que toute théorie qui admet un modèle infini se comporte à cet égard comme la théorie des corps commutatifs.

La notion d’extension élémentaire et la méthode des diagrammes permettent d’affiner ce résultat et d’en faire un très utile outil de construction de structures:

Théorème de Löwenheim-Skolem descendant (version Tarski-Vaught). Soit un cardinal infini au moins égal à celui de l’ensemble des symboles de L, face=F9828 b une L-structure, X un sous-ensemble de l’univers B de face=F9828 b, tels que |X| 諒 諒 |B|. Il existe une sous-structure élémentaire face=F9828 a de face=F9828 b dont l’univers A est de cardinal et tel que X 裂 A.

Enfin, en utilisant le théorème descendant et le théorème de compacité, on obtient le volet ascendant du théorème, dû en fait à Tarski:

Théorème de Löwenheim-Skolem ascendant. Soit face=F9828 a une L-structure infinie, un cardinal au moins égal au cardinal de L et au cardinal de A. Il existe une extension élémentaire face=F9828 b de face=F9828 a de cardinal .

En rapprochant les deux résultats, on voit notamment qu’une théorie admettant un modèle infini admet des modèles de tout cardinal infini (au moins égal à celui du langage).

Ultraproduits

Il est clair que le moyen le plus direct pour établir le théorème de compacité consisterait à fabriquer, à partir d’une famille de modèles des fragments finis d’une théorie T, un modèle de T. On est donc naturellement amené à rechercher des procédés de construction de modèles. On examine ici l’un des plus simples et des plus maniables de ces procédés.

Soit I un ensemble non vide et soit (face=F9828 aⁱ ), i 捻 I, une famille de L-structures. Un ultrafiltre sur I est un ensemble D de sous-ensembles de I qui vérifie les conditions suivantes:

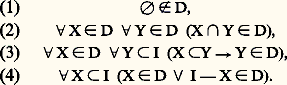À l’aide de D, on définit sur le produit direct:

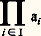la relation d’équivalence 令D suivante:

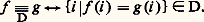L’ensemble quotient du produit direct des face=F9828 aⁱ par la relation d’équivalence 令D est désigné par:

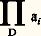et est appelé ultraproduit de la famille d’ensemble face=F9828 aⁱ (par rapport à l’ultrafiltre D). Pour définir l’ultraproduit:

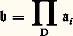de la famille de L-structures (face=F9828 aⁱ ), i 捻 I, il ne nous reste plus qu’à définir +^B , 練^B , 0^B et 1^B . On ne définira ici que +^B .

Soit f ^D, g ^D et h ^D des éléments de:

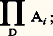On pose:

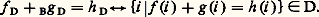Il est évident que:

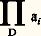est une L-structure. On admet le théorème suivant, dont la démonstration est aisée, une fois que l’on a défini de façon formelle la notion de vérité d’un énoncé dans une structure (ce que l’on n’a pas fait.)

Théorème de /Lo ご. Un énoncé 﨏 est vrai dans l’ultraproduit des face=F9828 aⁱ par rapport à l’ultrafiltre D si et seulement si l’ensemble des i tels que 﨏 soit vrai dans face=F9828 aⁱ appartient à D.

Dans le cas ou toutes les structures face=F9828 aⁱ coïncident avec une même structure face=F9828 a, l’ultraproduit:

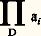est désigné par:

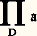et est appelé ultrapuissance de face=F9828 a. Il résulte immédiatement du théorème précédent que toute ultrapuissance d’une structure face=F9828 a est élémentairement équivalente à face=F9828 a.

Le théorème de /Lo ご conduit à une démonstration facile du théorème de Löwenheim-Skolem ascendant (sans appel à la compacité). Esquissons une démonstration d’un résultat un peu plus faible: une théorie de L qui admet un modèle infini face=F9828 a admet un modèle de tout cardinal au moins égal à celui de L et à celui de A. Il suffit d’établir que face=F9828 a est élémentairement équivalent à des L-structures de cardinal infini arbitrairement élevé. Compte tenu de ce qui précède, il suffit d’établir qu’il y a des ultrapuissances de face=F9828 a de cardinal arbitrairement grand. On y parvient en choisissant judicieusement l’ultrafiltre D.

On peut également déduire du théorème de /Lo ご une démonstration du théorème de compacité. Soit T une théorie et soit 杻 l’ensemble des sous-ensembles finis de T. On suppose que tout élément X de 杻 admet un modèle face=F9828 M^X et on se propose de montrer que T a un modèle. Pour tout élément X de 杻, on pose:

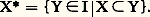Il est facile d’établir (grâce au lemme de Zorn) qu’il existe un ultrafiltre D sur 杻 auquel appartiennent tous les X. Désignons par face=F9828 M l’ultraproduit:

c’est un modèle de T: en effet, tout élément 﨏 de T est vrai dans face=F9828 M^Y pour tout Y 捻 﨏; l’ensemble des X tels que 﨏 est vrai dans face=F9828 M^X appartient donc à D. Par suite, 﨏 est vrai dans face=F9828 M. La démonstration est achevée.

Mentionnons enfin un très beau résultat qui a eu peu d’applications pratiques, encore qu’il permette de ramener la notion d’équivalence élémentaire à une notion, beaucoup plus familière aux mathématiciens, d’isomorphisme. Il s’agit donc certainement d’un résultat très important.

Théorème (Keisler-Shelah). Deux réalisations face=F9828 a et face=F9828 b sont élémentairement équivalentes si et seulement si elles admettent des ultrapuissances isomorphes: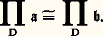

Types et omission des types

Dans les développements postérieurs à 1960, en particulier dans le théorème de Morley et ses prolongements (cf. Classification de modèles et complexité d’une théorie ), une notion centrale est celle de n-type d’une théorie complète T. C’est un ensemble p (en général infini) de formules de L, de variables libres v ¹, ..., v ⁿ , tel qu’il existe un modèle face=F9828 a de T contenant un n -uple (a ¹, ..., a ⁿ ) satisfaisant chaque formule de p (pour l’assignation de a ⁱ à v ⁱ ); nous exigeons de plus que p soit complet , au sens où, pour toute formule 﨏 en les variables v ¹, ..., v ⁿ , alors p a pour conséquence soit 﨏 soit 囹 﨏. Dans ces conditions, on dit que face=F9828 a réalise p et que le type de (a ¹, ..., a ⁿ ) est p . Dire que les éléments a et b de A ont même type dans face=F9828 a, c’est dire qu’il existe un automorphisme de face=F9828 a échangeant a et b .

Il est souvent nécessaire de considérer des types avec paramètres. Soit face=F9828 a une structure, X une partie de A. Un n -type (complet) au-dessus de X dans A est un n -type (complet) de la théorie de la structure [A, X] pour le langage L(X) obtenue à partir de A en interprétant c^x par x pour chaque x de X. Il existe donc une extension élémentaire face=F9828 b de face=F9828 a contenant un n -uple (a ¹, ..., a ⁿ ) satisfaisant chaque formule de p au sens de la structure [B, X]. Dans cette définition, on ne peut pas en général remplacer impunément face=F9828 a par une autre structure face=F9828 a contenant X. Il est cependant souvent possible de supposer, sans restreindre la généralité, que T permet l’élimination des quantificateurs dans le langage L (toute formule de L est équivalente modulo T à une formule sans quantificateur). Cette condition, que nous imposons désormais, permet de parler de n -type au-dessus de X, abstraction faite de face=F9828 a, et de structure contenant X qui ne réalise pas un n -type p au-dessus de X donné: on dit qu’elle omet le type p .

Prenons l’exemple de la théorie T^p des corps algébriquement clos de caractéristique p (où p fixé est premier ou nul). Soit X un sous-corps d’un modèle face=F9828 a de T^p . Les 1-types au-dessus de X sont, d’une part, les types d’éléments de A algébriques sur X: un tel type p est engendré par un polynôme P à coefficients dans X de plus bas degré tel que la formule P(v ¹) = 0 est dans p ; il n’est réalisé qu’un nombre fini fixé de fois dans tout surcorps de X modèle de T^p : on dit que p est algébrique . D’autre part, l’ensemble des formules P(v ¹) 0 pour tous les polynômes non nuls à coefficients dans X forme l’unique 1-type non algébrique dans S¹(X): c’est le type d’un élément transcendant sur X, qu’on ne trouve que dans une extension propre de A, c’est-à-dire que A omet le type p .

Le théorème fondamental suivant a été démontré, sous diverses formulations, par plusieurs logiciens au milieu des années 1950:

Théorème d’omission des types (Henkin, Orey et al.). Un type p 捻 Sⁿ (X) peut être omis dans un modèle de T si et seulement si p n’est pas principal, c’est-à-dire s’il n’existe pas de formule 﨏 telle que p soit l’ensemble des conséquences de 﨏 modulo T.

Ce résultat est équivalent au théorème d’ 諸-complétude (cf. théorie de la DÉMONSTRATION). D’autre part, il est fortement apparenté au forcing modèle-théorique, une méthode très féconde de construction de structures inventée vers 1970 par A. Robinson à partir du forcing ensembliste de Cohen (cf. théorie axiomatique des ENSEMBLES).

Citons deux applications du théorème d’omission des types.

Théorème de Ryll-Nardzewski. Une théorie T n’admet qu’un seul modèle dénombrable (à isomorphisme près) si et seulement si, pour chaque n , l’ensemble Sⁿ (face=F0019 歷) est fini.

Théorème de MacDowell-Specker. Soit face=F9828 b un modèle dénombrable de l’arithmétique de Peano (voir la partie Les théorèmes de limitation du chapitre Les notions fondamentales: la logique du premier ordre , in LOGIQUE – logique mathématique). Il existe une extension élémentaire face=F9828 b de face=F9828 a telle que B A et, pour tous b 捻 B 漣 A, a 捻 A, on a a 麗 b .

2. Classification des modèles et complexité d’une théorie

Théories catégoriques

C’est un vieux rêve de l’axiomatique que de caractériser intégralement une structure mathématique par un ensemble, aussi simple que possible, de conditions formelles. Dans le cadre de la théorie des modèles, cet idéal s’exprime très précisément ainsi: Soit L un langage (égalitaire), T une théorie de L; T est catégorique s’il n’existe, à l’isomorphisme près, qu’un seul modèle de T. Or on sait que le théorème de Löwenheim-Skolem a pour conséquence immédiate qu’une théorie ayant un modèle infini ne saurait être catégorique. Donc, si l’on s’intéresse aux théories de structures infinies, le seul espoir raisonnable est d’obtenir de T qu’elle soit -catégorique , pour un ou pour tout cardinal infini , c’est-à-dire qu’elle n’ait, à l’isomorphisme près, qu’un seul modèle de cardinalité .

Et, en effet, il existe de nombreux exemples de théories -catégoriques, pour une valeur, ou de multiples valeurs de . La théorie de l’égalité pure (dont les seuls axiomes sont ceux de l’égalité) est -catégorique pour tout ; il en est de même de la théorie des groupes infinis dont tout élément est d’ordre 2 (car ils peuvent être considérés comme des espaces vectoriels de dimension infinie sur Z/2Z), ou encore de la théorie du groupe (Z/4Z) 諸. La théorie d’un ordre dense sans extrêmes est -catégorique pour = 尿⁰ seulement (résultat dû à Cantor). La théorie des corps algébriquement clos de caractéristique p (où p est premier ou nul) est -catégorique pour tout non dénombrable, ainsi que la théorie des groupes abéliens divisibles et sans torsion.

De ces exemples /Lo ご dégage en 1954 la conjecture suivante:

Soit T une théorie dans un langage dénombrable. Si T est -catégorique pour un cardinal non dénombrable, T est -catégorique pour tout cardinal non dénombrable.

Cette conjecture est démontrée en 1962 par Morley. Les travaux de Morley n’ont pas seulement conduit à ce résultat magnifique; ils ont aussi apporté à la théorie des modèles un ensemble de concepts et de méthodes auxquels elle doit, dans une grande mesure, sa présente fécondité. C’est pourquoi, sans prétendre fournir ici de démonstration, on s’attachera à présenter quelques-unes de ses idées-forces.

Les grands axes de la démonstration de Morley

Étude des espaces S¹(X)

Nous proposons désormais que T est une théorie dans un langage dénombrable L, que T n’a pas de modèle fini, qu’elle est complète et permet l’élimination des quantificateurs dans L. Nous désignons par b une L-structure, par X un sous-ensemble de A.

Si Bⁿ (X) désigne le quotient de l’ensemble des formules de L(X) à n variables libres par la T(X)-équivalence (où T(X) est la théorie de (A, X), indépendante de face=F9828 a), alors l’ensemble Sⁿ (X) des n -types au-dessus de X est le stonien (c’est-à-dire l’ensemble des ultrafiltres) de Bⁿ (X): c’est un espace topologique compact et totalement discontinu dont une base d’ouverts-fermés est constituée par les U size=1^﨏 =p ; 﨏 捻 p, avec 﨏 捻 Bⁿ (X). Les types principaux sont les points isolés de Sⁿ (X).

Deux idées profondément originales, dues à Morley, orientent cette étude: l’une se fonde sur la cardinalité, l’autre sur l’opération de dérivation de Cantor-Bendixson.

La première part de la définition suivante: Soit un cardinal infini: T est-stable si, pour toute partie X d’un modèle de T,

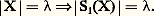Morley établit les implications suivantes:

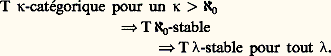La seconde idée consiste à classer les éléments de S¹(X) selon leur degré d’«isolement» relatif. Un élément isolé p de S¹(X) a pour rang de Cantor-Bendixson CB(p ) = 0; un élément isolé p de l’espace S¹(X) privé de ses éléments de rang 0 a pour rang CB(p ) = 1, et ainsi de suite par induction transfinie. Enfin, le rang de Morley d’un type p est défini comme:

où le sup est pris sur les éléments p 捻 S¹ (Y) tels que X 說 Y et p 說 p .

Morley montre que, si T est 尿⁰-stable, tout type a un rang de Morley bien défini.

Indiscernables

Ehrenfeucht et Mostowski ont dégagé la notion centrale d’ensemble ordonné indiscernable I dans une structure face=F9828 a: I est une partie totalement ordonnée de A (l’ordre n’étant pas nécessairement définissable dans face=F9828 a) dont, pour chaque n , tous les n -uples strictement croissants ont le même n -type; autrement dit, si i ¹ 麗 ... 麗 i ⁿ et i ¹ 麗 ... 麗 i ⁿ sont des éléments de I, on a dans A:

pour toute formule 﨏 à n variables de L.

Il résulte du théorème combinatoire de Ramsey que, étant donné une théorie T et un ensemble ordonné infini I, il existe un modèle de T dans lequel I est indiscernable. On peut même obtenir des modèles qui sont engendrés (à l’aide des fonctions) par un ensemble ordonné indiscernable. De tels modèles ont d’étonnantes propriétés, dont celle d’admettre de nombreux automorphismes et de posséder des sous-structures et des extensions élémentaires qui leur ressemblent très fortement.

Morley découvre notamment que, si T est 尿⁰-stable, tout ensemble ordonné indiscernable I d’un modèle T est en fait indiscernable abstraction faite de son ordre: toute formule à n variables est simultanément vérifiée ou falsifiée par tous les n -uples d’éléments distincts de I.

Modèles premiers

Soit face=F9828 a un modèle de T et X une partie de A. On dit que face=F9828 a est premier au-dessus de X si face=F9828 a se plonge élémentairement au-dessus de X (le plongement laissant fixe tout x 捻 X) dans tout modèle de T contenant X. Morley montre que, si T est 尿⁰-stable, un modèle premier existe au-dessus de tout X. Plus tard, Shelah établira, sous les mêmes hypothèses, l’unicité, pour X donné, du modèle premier au-dessus de X.

Modèles saturés

Un modèle premier (au-dessus de X) est pauvre, au sens où il réalise peu de types (au-dessus de X). L’idée opposée de modèle riche a été précisée par Morley et Vaught: une structure face=F9828 a est-saturée si, pour toute partie X de A telle que |X| 麗, tout n -type au-dessus de X, pour tout n , est réalisé dans face=F9828 a. Une étape de la démonstration de la conjecture de /Lo ご consiste à montrer qu’une théorie 尿⁰-stable possède pour tout 礪 尿⁰ un modèle 尿¹-saturé de cardinalité . La-saturation est une notion très importante, qui trouve son origine et ses premiers exemples dans les ordres denses 兀 size=1^見 de Hausdorff, lesquels sont précisément 尿 size=1^見-saturés.

Théories stables; les travaux de Shelah

Résolution complète du cas catégorique

Le théorème de Morley appelait deux grandes questions, dont la solution a exigé le développement d’une nouvelle théorie, prolongeant celle de Morley, centrée sur la notion de stabilité. Ce travail est dû, au premier chef, à S. Shelah.

La première question était de confirmer une conjecture de Vaught, selon laquelle une théorie 尿¹-catégorique possède soit un seul, soit 尿⁰ modèles dénombrables: Baldwin et Lachlan y parvinrent en 1970. La seconde question était d’étendre le résultat de Morley aux théories (de langages) non dénombrables. C’est ce que Shelah réussit la même année: Si une théorie de langage L est -catégorique pour un cardinal 礪 |L|, cette théorie est -catégorique pour tout cardinal 礪 |L| où |L| désigne le cardinal de l’ensemble des formules de L.

Classification et dénombrement des modèles

Les théories (dénombrables) 尿¹-catégoriques sont d’une extrême simplicité du triple point de vue du nombre de leurs modèles , de la classification de leurs modèles (un modèle face=F9828 a est caractérisé par sa dimension , qui est un cardinal 嗀, comparable au degré de transcendance pour les corps et à la dimension pour les espaces vectoriels, tel que 嗀 + 尿⁰ = |A|), enfin de celui du nombre de leurs types avec paramètres. Ce cas étant entièrement élucidé, il est naturel de chercher une corrélation entre ces différentes mesures de la complexité d’une théorie. C’est ce à quoi s’est attaché Shelah, avec un succès presque complet.

Un premier problème est de déterminer quel peut être le spectre de stabilité d’une théorie T, c’est-à-dire l’ensemble St(T) des cardinaux tels que T est-stable. Shelah (1971) montre qu’il n’y a que quatre spectres possibles, par ordre croissant de complexité de la théorie:

– le spectre des théories 尿⁰-stables est la collection des cardinaux;

– le spectre des théories superstables est| 閭 2 size=1^尿0;

– le spectre des théories stables est| size=1^尿0 =;

– le spectre des théories instables est vide.

Il existe de nombreux exemples de chaque espèce, notamment parmi les théories algébriques usuelles. Les théories instables se divisent à leur tour en trois groupes (Keisler, 1976), selon la valeur de sup |S(A)|, où A est modèle de T et |A| = .

C’est ainsi qu’on parvient à cerner le problème de la classification des modèles . Le but poursuivi, de manière générale, est d’exhiber un critère de classification des modèles de T (par un cardinal tel que la dimension, ou une famille plus ou moins complexe de cardinaux) ou, à défaut, de montrer, en un sens à préciser, que les modèles de T échappent à toute classification.

Enfin, on espère lier la classification des modèles à leur dénombrement, et déterminer la forme des applications f ^T: 料 nombre de modèles de T de cardinal. L’idée maîtresse est qu’une théorie dont les modèles sont classifiables n’en possède pas trop; plus précisément, on espère établir l’existence de tel que f ^T() 麗 2 size=1^凞. De grands progrès ont été accomplis en ce sens par Shelah. Le phénomène inverse est illustré par le théorème suivant, encore dû à Shelah (1971): Une théorie non superstable a 2 size=1^凞 modèles en tout cardinal non dénombrable .

Il n’est guère possible d’exposer ici les méthodes employées. Indiquons cependant qu’elles trouvent encore leur source dans les travaux de Morley. Elles comprennent, d’une part, une analyse très fine des types à l’aide de la notion de bifurcation (due à Shelah), qui étend celle d’indépendance linéaire (dans les espaces vectoriels) ou algébrique (dans les corps), et, d’autre part, des principes de construction de modèles jouant le rôle soit de modèle pauvre, soit de modèle riche, soit de modèle engendré par indiscernables.

3. Théorie des modèles et mathématiques

Théorie des modèles et algèbre traditionnelle

Il devrait être maintenant clair que les débuts de la théorie des modèles sont assez voisins de l’algèbre générale. Il n’est donc pas étonnant qu’il y ait eu de nombreuses applications de cette théorie à des problèmes purement algébriques. Il faut cependant dire que les premières applications «essentielles» de la théorie des modèles à l’algèbre datent de la fin des années cinquante. Jusque-là, les techniques logiques permettaient d’étudier les propriétés «locales» des structures algébriques, c’est-à-dire celles qui mettent en jeu les sous-structures de type fini, et surtout d’apporter un nouvel éclairage et d’intéressants compléments aux résultats classiques sur les corps algébriquement clos et aux travaux de E. Artin sur les corps réels fermés. L’expérience ainsi acquise fut certainement précieuse dans le premier des développements que l’on va évoquer.

– Travaux sur les corps p-adiques. Ces recherches donnèrent lieu à une démonstration du résultat suivant conjecturé par Artin: pour chaque entier positif d , il y a un nombre premier p (d ) tel que, pour tout nombre premier p 閭 p (d ), tout polynôme homogène sur le corps des nombres p -adiques Q^p , de degré d et ayant au moins d ² + 1 variables, admet un zéro non trivial dans Q^p . À vrai dire, la conjecture d’Artin dans sa forme initiale affirmait que le résultat précédent devait être vrai pour tous les nombres premiers p . On sait aujourd’hui que cette conjecture est fausse, ce qui accroît considérablement l’intérêt que présente le résultat précédent, dont la seule démonstration existante utilise les techniques de la théorie des modèles.

– Recherche d’invariants. Le logicien qui, pour simplifier, ne distingue pas entre deux réalisations élémentairement équivalentes est particulièrement heureux de trouver des invariants qui caractérisent l’équivalence élémentaire , autrement dit d’attacher à une structure face=F9828 A un objet h (face=F9828 A), défini de préférence de façon purement mathématique (c’est-à-dire dont la définition ne fait pas appel à un langage privilégié tel que celui du premier ordre) et aussi simple que possible tel que, pour des structures face=F9828 B et face=F9828 C, les objets h (face=F9828 B) et h (face=F9828 C) coïncident si et seulement si les structures face=F9828 B et face=F9828 C sont élémentairement équivalentes. Le mathématicien préférerait trouver des invariants qui caractérisent l’isomorphisme. Il convient d’observer que ce dernier problème est sans doute bien plus difficile que le premier, car il n’y a par exemple pas de théorème de Cantor-Bernstein pour l’isomorphisme (deux groupes commutatifs dont chacun est isomorphe à un facteur direct de l’autre ne sont pas toujours isomorphes), alors qu’il y a un théorème de Cantor-Bernstein pour l’équivalence élémentaire; et, de fait, le logicien a résolu son problème dans beaucoup plus de cas (groupes commutatifs, groupes de type fini «presque commutatifs», algèbres de Boole) que le mathématicien (groupes commutatifs dénombrables de torsion: la solution est connue sous le nom de théorème d’Ulm ).

La classification des structures à isomorphisme près est l’un des principaux objectifs de la théorie de la stabilité fondée par Shelah et discutée ci-dessus, et ces deux problèmes appartiennent maintenant à la théorie des modèles.

D’autres développements récents ont montré que les deux problèmes n’étaient pas très éloignés l’un de l’autre. On a introduit le langage L size=1^秊 size=1^諸, qui est défini comme le langage du premier ordre L utilisé dans cet article, à cela près qu’on y autorise la formation de conjonctions et disjonctions infinies. On peut alors démontrer que des structures dénombrables ont la même théorie pour ce langage si et seulement si elles sont isomorphes. On peut essayer de trouver des invariants pour l’analogue de l’équivalence élémentaire dans le langage L size=1^秊 size=1^諸, ce qui permet d’établir une généralisation du théorème d’Ulm. Les mêmes idées ont permis de justifier dans une certaine mesure le principe empirique suivant lequel, quand on fait de la géométrie algébrique sur un corps algébriquement clos de caractéristique zéro, on peut se borner à considérer le corps des nombres complexes.

Le problème de la recherche d’invariants pour l’équivalence élémentaire est également lié à un des problèmes fondamentaux de la logique: celui de la décidabilité (cf. la partie Décidabilité du chapitre Les notions fondamentales : la logique du premier ordre , in LOGIQUE MATHÉMATIQUE). Encore qu’on ne connaisse pas de théorème général, il est facile, dans plusieurs cas particuliers, dont celui de la théorie des groupes commutatifs, de déduire des invariants obtenus la décidabilité de la théorie.

D’autres travaux débordent le cadre de l’algèbre classique et peuvent, avec quelque artifice, être classés sous deux rubriques aux interconnections de plus en plus étroites.

La théorie des modèles envahit de nouveaux domaines

La théorie des modèles a permis d’approfondir la théorie des corps différentiels et envahit peu à peu la théorie des nombres, l’analyse, la géométrie algébrique et la théorie des catégories.

La démonstration par J. Ax de l’existence d’un algorithme pour la solubilité modulo p , pour tout premier p , des équations diophantiennes et la démonstration par Matijasevi face="EU Caron" カ de l’inexistence d’un algorithme pour la solubilité en nombres entiers de ces équations ont eu une descendance nombreuse. L’utilisation de l’hypothèse de Riemann pour les courbes avait déjà permis à Ax d’établir la décidabilité de la théorie des corps finis. En utilisant les corps hilbertiens et les groupes pro-finis, ainsi qu’un soupçon de théorie des modèles, on a généralisé de façon naturelle ce résultat. Ces travaux ont contribué à remettre à l’honneur l’algèbre effective et à poursuivre dans la voie tracée par A. Robinson, en donnant des démonstrations logiques des résultats classiques de cette discipline (algorithme permettant de reconnaître si un polynôme appartient à un idéal, etc.). Dans la direction opposée, un peu de géométrie algébrique et beaucoup de finesse avaient permis à Raphael Robinson de démontrer, en 1963, l’indécidabilité de la théorie du corps R(X). Il était naturel, à la lumière du résultat de Matijasevi face="EU Caron" カ, d’examiner le fragment des énoncés purement existentiels de cette théorie et de bien d’autres. Si les techniques logiques sont tout aussi élémentaires, les résultats utilisés sur les courbes algébriques sont bien plus complexes; mais le cas des énoncés existentiels vrais dans le corps des rationnels est toujours ouvert.

– Analyse non standard . En considérant une ultrapuissance convenable du corps des nombres réels R, on obtient un corps réel fermé non archimédien élémentairement équivalent à R ^{[cf. ANALYSE NON STANDARD]}. On est parvenu en raffinant cette construction à fonder le calcul différentiel classique sur les infinitésimaux. Cette façon de faire a un intérêt historique et pédagogique considérable. En fait, une nouvelle branche de la mathématique est peut-être née, dont les applications sont déjà nombreuses.

Si l’enthousiasme manifesté par quelques praticiens n’est pas toujours partagé par l’ensemble de la communauté logique, certaines applications très concrètes aux équations différentielles sont indéniablement fort séduisantes.

Des techniques logiques plus fines (théorie des nombres non standard) ont permis à A. Robinson et P. Roquette de donner une démonstration du théorème de finitude de Siegel et Mahler qui a l’apparence de la nouveauté.

Alors que ces travaux utilisent la géométrie algébrique, il en est d’autres qui visent à étudier de façon modèle-théorique la géométrie algébrique. Il y a une littérature considérable d’inspiration classique qui étend aux faisceaux, sous des hypothèses restrictives, les résultats relatifs aux produits. Les travaux les plus novateurs sont sans doute ceux qui étudient de façon modèle-théorique la théorie des topos (on pourra consulter l’ouvrage de M. Makkai et G. Reyes, «First-order categorical logic; model-theoretical methods in the theory of topoi and related categories», in Lecture Notes in Mathematics , Springer-Verlag, Berlin, 1977).

La logique a permis d’approfondir la théorie des corps différentiels, d’origine algébrique, en dégageant la notion de corps différentiel clos . Un corps différentiel est un corps (commutatif) muni d’une opération de dérivation D vérifiant les axiomes: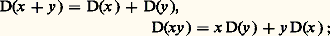

cette notion est la généralisation naturelle du corps des fractions rationnelles à une variable sur un corps, muni de la dérivation formelle habituelle. Un tel corps est dit différentiel clos si tout système différentiel «raisonnable» possède une solution. Dans ce domaine, les progrès les plus spectaculaires ont découlé très simplement des travaux de Morley. La théorie des corps différentiels clos de caractéristique zéro est 尿⁰-stable, ce qui permet de répondre immédiatement aux questions anciennes sur les modèles premiers. Le cas de la caractéristique p est plus complexe et a suscité un théorème difficile de pure théorie des modèles qui est dû à Shelah. Ainsi, la théorie des corps différentiels, à la fois, a bénéficié de la théorie de la stabilité et l’a fait progresser (une version soigneusement expurgée de toute formulation modèle-théorique est due à Kolchin). La théorie des corps différentiels a également été un champ d’application de la théorie des modèles récursive où on s’intéresse à la construction de modèles récursifs .

Théorie des modèles et stabilité

On a indiqué plus haut l’impact de la théorie de la stabilité sur la théorie des corps différentiels. La théorie de la stabilité est également intervenue en algèbre en ce qu’on s’est attaché à inventorier les structures algébriques stables, 尿⁰-stables, etc. On a d’abord montré que les corps 尿⁰-stables n’étaient autres que les corps algébriques clos et puis, selon une ligne traditionnelle, on a tenté de ramener le cas des anneaux à celui des corps. L’étude des groupes linéaires débouche évidemment sur celle des corps. Les résultats les plus intéressants touchent les groupes localement finis. On a montré qu’il existe une grande variété de groupes localement finis universels homogènes (cf. P. Hall, J. London Math. Soc. , 1959). On a également réussi à caractériser les groupes, nécessairement localement finis, dont la théorie est catégorique en tout cardinal (infini). Cette caractérisation utilise les techniques de la théorie des groupes localement finis, elle-même fondée sur la théorie des groupes finis, et la théorie de la stabilité. Il s’avère que, dans l’étude des structures algébriques stables, des conditions de chaîne analogues aux conditions classiques de Noether interviennent, mais où la définissabilité joue un rôle capital.

Il convient de signaler ici quelques résultats brillants qui se rattachent partiellement, par les techniques combinatoires utilisées, aux considérations précédentes. Vers 1974, Shelah a démontré les premiers résultats explicites d’indépendance en algèbre. Il a établi que l’on ne pouvait ni démontrer ni réfuter dans la théorie des ensembles de Zermelo-Fraenkel une foule de conjectures relatives aux groupes presque libres. La démonstration de Shelah, qui n’a pas grand-chose à voir avec la théorie des modèles générale, utilise un principe combinatoire dit du diamant, mis en évidence par Jensen dans son étude des ensembles constructibles, et un nouveau principe de compacité qui affirme, en particulier, qu’un groupe de cardinal singulier 見 (cf. théorie des ENSEMBLES – Théorie axiomatique des ensembles) est libre dès que tous ses sous-groupes de cardinal strictement inférieur à 見 sont libres. Un argument combinatoire voisin de ceux qui interviennent dans la théorie de la stabilité a également permis à Shelah de répondre à une question ancienne sur les algèbres de Jónsson en montrant l’existence de groupes non dénombrables dont tout sous-groupe propre est dénombrable.

D’une nature toute différente est le résultat de Harrington et Paris ^{[cf. RÉCURSIVITÉ]}, qui réalise pour l’arithmétique un peu ce que Cohen avait fait pour la théorie des ensembles. Il existe maintenant plusieurs démonstrations de leur résultat (cf. Jon Barwise, Handbook of Mathematical Logic , North Holland, Amsterdam, 1977), dont l’une est modèle-théorique. Une nouvelle combinatoire est née, et le calcul des pseudo-nombres de Ramsay a déjà des adeptes, dont des ordinateurs.

Et l’avenir?

D’ores et déjà, une compréhension accrue des structures mathématiques élaborées a été obtenue en utilisant la théorie de la stabilité; ainsi Zilber a-t-il obtenu une démonstration modèle-théorique d’un théorème de Borel-Tits relatif aux isomorphismes des groupes algébriques simples (d’où l’on peut, réciproquement, déduire la 尿¹-catégoricité de ces groupes). La classification des groupes stables semble être intimement liée à l’étude des groupes algébriques. De simples considérations de définissabilité ont permis de trivialiser les rudiments de la géométrie algébrique classique, puis d’élaborer de façon plus fine une véritable géométrie algébrique réelle. Ce concept de définissabilité, qui joue un rôle fondamental dans la théorie de la stabilité, est également primordial dans l’étude de théories naturelles instables telles que l’arithmétique. Des idées issues de la théorie de la stabilité ont été appliquées avec succès aux espaces de Banach. Il sera de plus en plus difficile aux mathématiciens d’ignorer l’arsenal de la théorie des modèles, mais il s’agira d’une théorie des modèles très large, empiétant sur la théorie descriptive des ensembles et sur la théorie de la récursivité, et débordant le cadre étroit de la logique du premier ordre.

Encyclopédie Universelle. 2012.